Dãy số Fibonacci không chỉ là một khái niệm nổi bật trong toán học mà còn là một chuỗi số huyền bí xuất hiện khắp nơi trong tự nhiên, nghệ thuật và cả công nghệ hiện đại. Nếu bạn từng tự hỏi: Dãy Fibonacci là gì? Vì sao nó được nhắc đến nhiều như vậy? – thì bài viết này chính là lời giải đáp đầy đủ và chi tiết nhất.
Dãy số Fibonacci là gì?
Dãy Fibonacci là một chuỗi số trong đó mỗi số (từ số thứ ba trở đi) bằng tổng của hai số đứng trước nó. Dãy số bắt đầu bằng:
Công thức tổng quát:
-
F(0) = 0
-
F(1) = 1
-
F(n) = F(n – 1) + F(n – 2) (với n ≥ 2)
Đặc điểm nổi bật của dãy số này là: Càng về sau, tỉ lệ giữa hai số liên tiếp càng tiến gần đến một giá trị cố định là 1.6180339887… – còn được gọi là tỷ lệ vàng (Golden Ratio).
Nguồn gốc lịch sử của dãy Fibonacci
Dãy số này được đặt theo tên của nhà toán học người Ý Leonardo Fibonacci (1170 – 1250), người đã giới thiệu nó trong cuốn sách nổi tiếng Liber Abaci xuất bản năm 1202. Trong cuốn sách, ông dùng dãy số này để giải một bài toán mô hình hóa sự phát triển dân số thỏ – từ đó, một phát hiện toán học mang tính cách mạng ra đời.
Ví dụ bài toán thỏ:
Nếu một cặp thỏ sinh sản sau một tháng và tiếp tục sinh sản mỗi tháng sau đó, thì sau 12 tháng sẽ có bao nhiêu cặp thỏ?
=> Kết quả chính là các số Fibonacci.
Tỷ lệ vàng và mối liên hệ với Fibonacci
Tỷ lệ giữa hai số liên tiếp trong dãy Fibonacci (bắt đầu từ số lớn) tiệm cận dần đến 1.618…, gọi là tỷ lệ vàng. Đây là con số đã được sử dụng suốt hàng nghìn năm để tạo nên vẻ đẹp cân đối trong nghệ thuật, kiến trúc và cả cơ thể con người.
Tỷ lệ vàng = (1 + √5) / 2 ≈ 1.6180339887
Bạn có thể thấy tỷ lệ này trong:
-
Kim tự tháp Giza (Ai Cập)
-
Bức tranh “Vitruvian Man” của Leonardo da Vinci
-
Các logo nổi tiếng như Apple, Twitter, Pepsi
Ứng dụng của dãy Fibonacci trong cuộc sống
Trong thiên nhiên
Fibonacci xuất hiện một cách tự nhiên nhưng có quy luật rõ ràng:
-
Số cánh hoa thường là số Fibonacci: hoa cúc có 34, 55 hoặc 89 cánh
-
Cấu trúc hạt hướng dương, quả dứa, vỏ ốc xoắn – đều có dạng hình xoắn ốc vàng (golden spiral)
-
Cành cây mọc theo dãy Fibonacci để tối ưu hóa ánh sáng mặt trời
Trong tài chính và chứng khoán
Dãy Fibonacci đóng vai trò quan trọng trong phân tích kỹ thuật:
-
Công cụ Fibonacci retracement giúp xác định các mức hỗ trợ – kháng cự trong biểu đồ giá
-
Các tỷ lệ 23.6%, 38.2%, 61.8%, 78.6% thường được nhà giao dịch sử dụng để dự đoán điểm đảo chiều hoặc hồi phục giá
Trong thiết kế, nghệ thuật và âm nhạc
-
Tỷ lệ vàng từ dãy Fibonacci giúp bố cục hình ảnh, tranh vẽ, logo trở nên hài hòa và cân đối hơn
-
Nhiều bản nhạc kinh điển như của Mozart, Beethoven có cấu trúc âm nhạc dựa theo quy luật Fibonacci
-
Trong nhiếp ảnh, kỹ thuật chia bố cục khung hình theo tỷ lệ vàng được áp dụng để tạo chiều sâu và sự cuốn hút
Trong lập trình và khoa học máy tính
-
Dãy Fibonacci là ví dụ điển hình khi dạy về thuật toán đệ quy
-
Một số thuật toán tìm kiếm, phân tích hiệu suất và nén dữ liệu cũng sử dụng nguyên lý Fibonacci
-
Thậm chí, trong blockchain, một số mô hình cũng áp dụng thuật toán này để điều chỉnh mức độ phân quyền hoặc phần thưởng
Dãy Fibonacci trong văn hóa và tôn giáo
Trong một số nền văn minh và tôn giáo, Fibonacci được coi là một biểu tượng của sự hoàn hảo:
-
Trong kiến trúc Thiên Chúa giáo cổ, nhiều nhà thờ, tháp chuông được xây dựng theo tỷ lệ vàng
-
Cuốn tiểu thuyết “The Da Vinci Code” của Dan Brown cũng gợi nhắc đến chuỗi Fibonacci như một phần của mật mã cổ đại đầy bí ẩn
-
Nhiều học giả còn liên hệ tỷ lệ vàng với “dấu vết của Thượng đế” trong sáng tạo vũ trụ
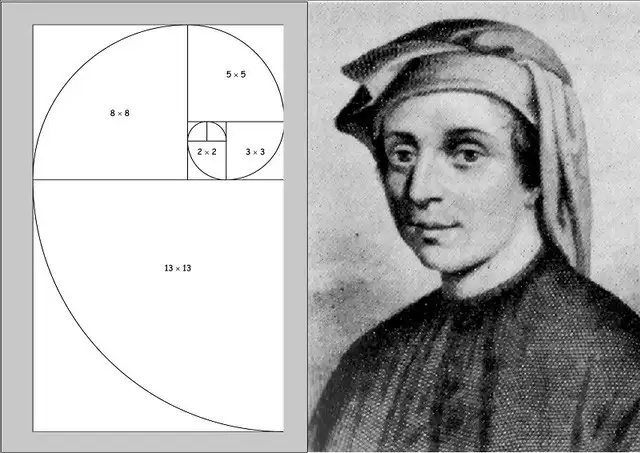
Một số con số Fibonacci phổ biến
| Vị trí (n) | Số Fibonacci (F(n)) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 20 | 6765 |
| 30 | 832040 |
Kết luận: Vì sao dãy Fibonacci luôn hấp dẫn?
Dãy số Fibonacci không chỉ là một chuỗi số mang tính toán học, mà còn là một biểu tượng cho sự hài hòa, trật tự và vẻ đẹp hoàn hảo trong tự nhiên và cuộc sống. Từ những bông hoa đến thị trường chứng khoán, từ kiến trúc cổ đến công nghệ hiện đại – Fibonacci vẫn luôn hiện diện như một quy luật bất biến và kỳ diệu.
“Mọi sự sống quanh ta đều mang một nhịp điệu – và đôi khi, nhịp điệu ấy lại là dãy Fibonacci.”
