Hỗn số là gì? Ví dụ và bài tập minh họa

Hỗn Số Là Gì?

Hỗn số là một cách biểu diễn số học kết hợp giữa một số nguyên và một phân số nhỏ hơn 1. Hỗn số được viết dưới dạng: số nguyên + phân số, trong đó phân số có tử số nhỏ hơn mẫu số (phân số tối giản).

Ví dụ:

• 2 ½ (đọc là: hai và một phần hai).

• 5 ¾ (đọc là: năm và ba phần tư).

Hỗn số thường được sử dụng để biểu diễn các giá trị không tròn, dễ hiểu hơn trong thực tế so với phân số.

---

Cách Chuyển Phân Số Sang Hỗn Số

Để chuyển một phân số lớn hơn 1 (tử số lớn hơn mẫu số) thành hỗn số, thực hiện các bước sau:

1. Chia tử số cho mẫu số để lấy nguyên và dư.

2. Số nguyên là phần nguyên của hỗn số.

3. Dư là tử số mới, mẫu số giữ nguyên.

Ví dụ: Chuyển phân số 17/5 thành hỗn số.

• 17 chia 5 được 3 (phần nguyên), dư 2.

• Hỗn số: 3 2/5.

Bài tập minh họa:
Chuyển các phân số sau thành hỗn số:

1. 22/7

2. 15/4
   Đáp án:

3. 22 ÷ 7 = 3 dư 1 → 3 1/7.

4. 15 ÷ 4 = 3 dư 3 → 3 3/4.

---

Đổi Từ Hỗn Số Sang Phân Số

Để chuyển hỗn số thành phân số, thực hiện các bước sau:

1. Nhân phần nguyên với mẫu số, sau đó cộng với tử số.

2. Giữ nguyên mẫu số.

3. Kết quả là phân số tương ứng.

Ví dụ: Chuyển hỗn số 4 2/3 thành phân số.

• 4 × 3 + 2 = 12 + 2 = 14.

• Phân số: 14/3.

Bài tập minh họa:
Chuyển các hỗn số sau thành phân số:

1. 3 1/2

2. 5 2/5
   Đáp án:

3. 3 × 2 + 1 = 7 → 7/2.
4. 5 × 5 + 2 = 27 → 27/5.

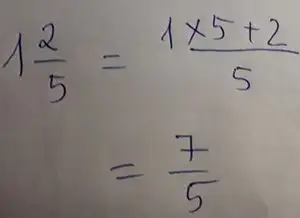
Phép Tính Toán Học Trên Hỗn Số

1. Cộng và trừ hỗn số

• Cách làm: Chuyển hỗn số thành phân số, thực hiện phép tính, sau đó chuyển lại thành hỗn số (nếu cần).

• Ví dụ: 2 1/3 + 1 2/5.

  • Chuyển: 2 1/3 = 7/3; 1 2/5 = 7/5.

  • Quy đồng mẫu số: 7/3 = 35/15; 7/5 = 21/15.

  • Cộng: 35/15 + 21/15 = 56/15 = 3 11/15.

2. Nhân và chia hỗn số

• Cách làm: Chuyển hỗn số thành phân số, thực hiện nhân hoặc chia như phân số thông thường.

• Ví dụ: 2 1/2 × 1 1/3.

  • Chuyển: 2 1/2 = 5/2; 1 1/3 = 4/3.

  • Nhân: (5/2) × (4/3) = 20/6 = 3 1/3.

Bài tập minh họa:

1. Tính: 3 1/4 + 2 2/3.

2. Tính: 4 1/5 × 2 1/2.
   Đáp án:

3. 3 1/4 = 13/4; 2 2/3 = 8/3. Quy đồng: 13/4 = 39/12; 8/3 = 32/12.
   Cộng: 39/12 + 32/12 = 71/12 = 5 11/12.

4. 4 1/5 = 21/5; 2 1/2 = 5/2. Nhân: (21/5) × (5/2) = 105/10 = 10 1/2.

---

Kết Luận

Hỗn số là một dạng biểu diễn số tiện lợi, dễ hiểu, được sử dụng phổ biến trong toán học và thực tế. Việc nắm vững cách chuyển đổi giữa hỗn số và phân số, cùng với các phép tính cơ bản, giúp giải quyết các bài toán một cách chính xác và hiệu quả.

Xem thêm tại: Thư viện khoa học